图网络入门

GPT摘要

这篇文章介绍了图神经网络（GNN）的基础概念和实现方法。主要内容包括： 1. 图的表示方式：介绍了邻接矩阵和邻接表两种表示方法，并分析了它们在空间效率和稀疏性上的差异。顶点、边和全局信息可以用向量表示，而连接信息通过邻接结构体现。 2. 图数据的应用场景：讨论了图片、文本、分子结构和社交网络等不同类型的数据如何用图表示，并展示了图级别（如判断环路）、节点级别（如社交网络中的影响力分析）和边级别（如物体关系判断）的任务示例。 3. GNN的核心机制：通过消息传递神经网络（MPNN）实现层间信息传递，置换不变性是关键特性。文章强调聚合操作（如池化）和邻域聚合（如GCN）的作用，包括点边信息的交互更新和引入全局节点（master node）以解决长距离依赖问题。 4. 实现细节与优化：提供了PyTorch的GCN实现代码示例，涵盖邻接矩阵归一化、自环添加和多层传播过程。还讨论了超参数选择（如嵌入维度、层数）和注意力机制（如加权聚合与内积评分）。 5. 扩展与改进：提到了超图、随机游走采样等技术，以及如何通过增加复杂特征（如边与全局信息的融合）提升模型表现力。

https://distill.pub/2021/gnn-intro/

  • 图的矩阵表示
    • 邻接矩阵
    • 邻接表：稀疏性
  • 聚合操作：实现层间的信息传递
    • 层内：池化
    • 层间：GCN邻域聚合、考虑邻接节点的权重（attention） 先采样再聚合

image-20230524214233460

什么数据会用图表示 图数据有什么特点区别，构建一个GNN，提供一个GNN playground

图表示

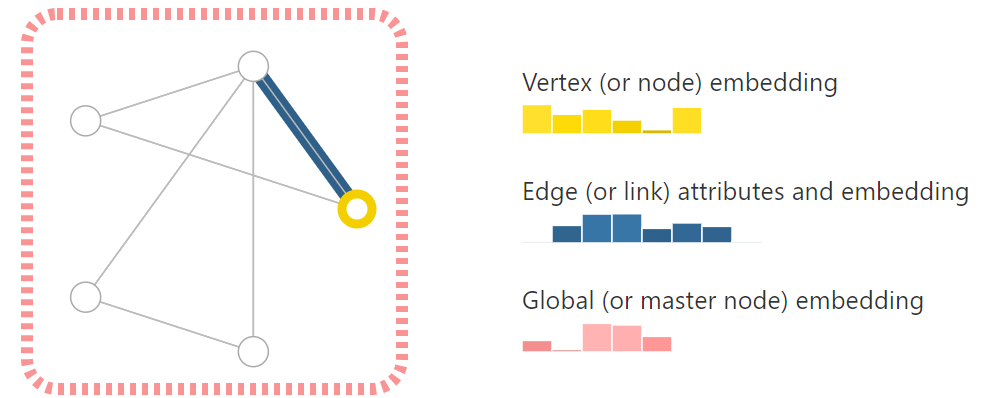
顶点、边、全局 用向量来表示。内部有信息，通过向量存储

image-20230524214810624

image-20230524215123040

什么能被表示为图

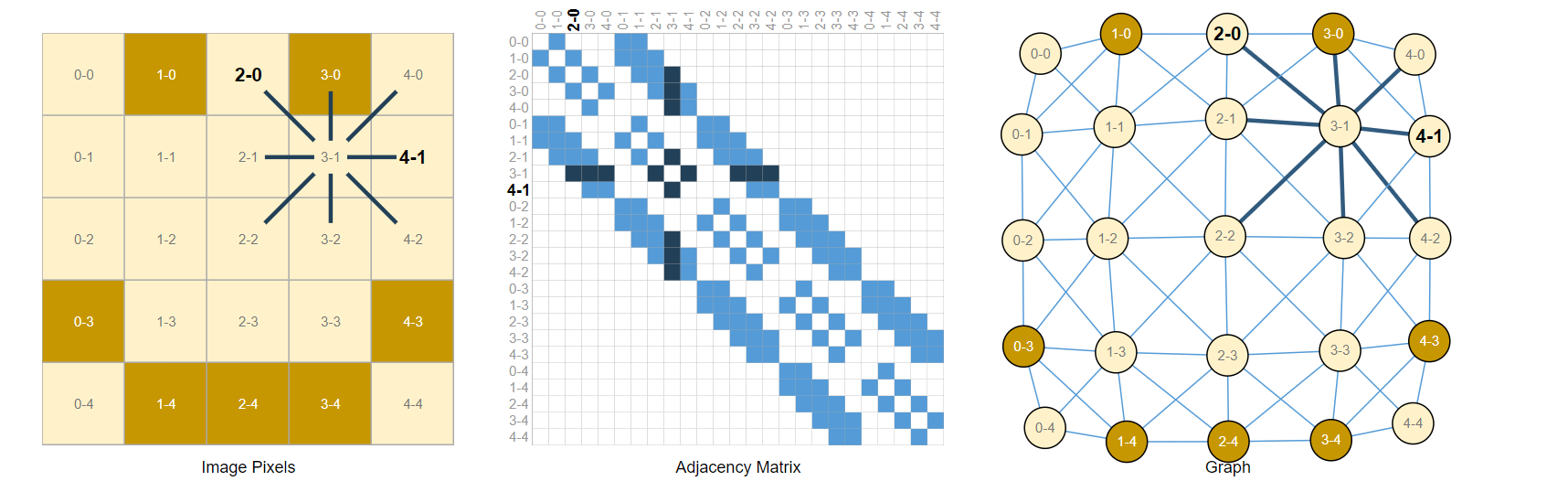
图片表示为图

image-20230524215156969

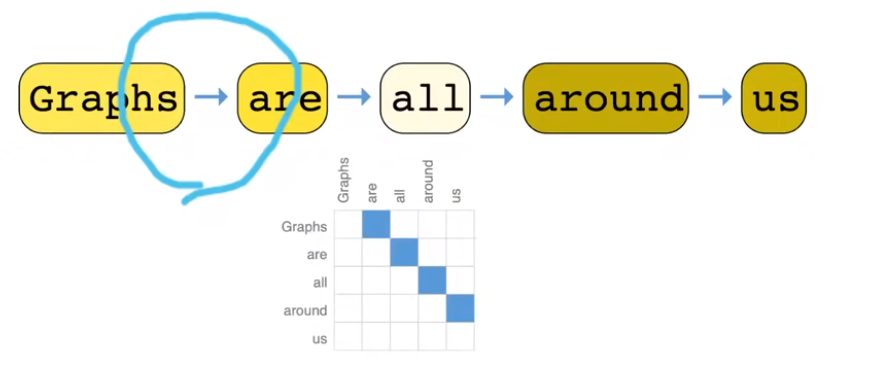
文本

image-20230524215642756

分子 Molecules

image-20230525095851988

社交关系图

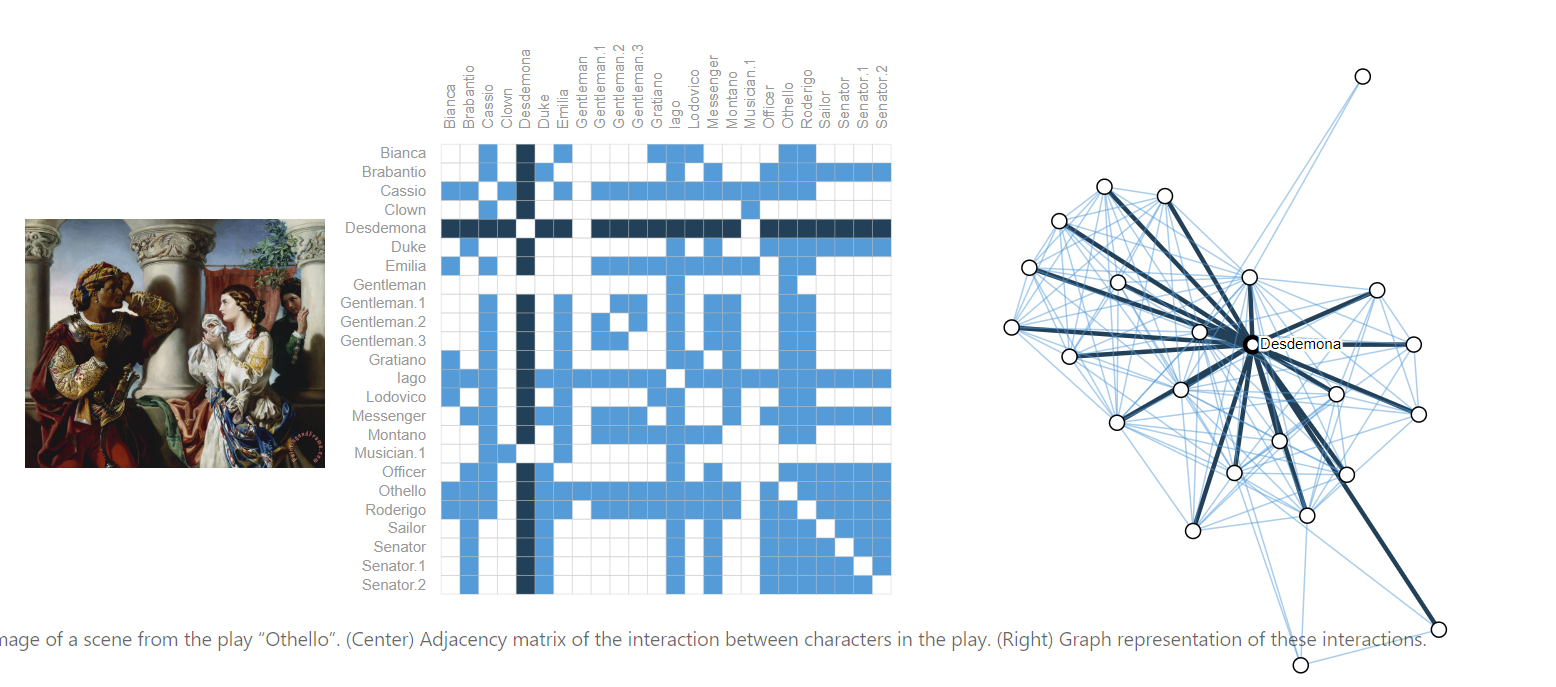
image-20230524215744881

引出什么问题

graph-level, node-level, and edge-level

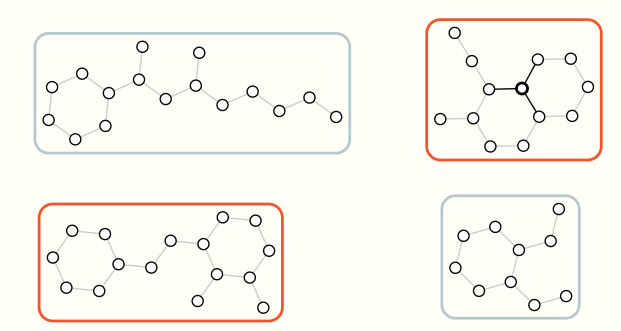
  • 对整个图判断：是否有环
image-20230525100550222
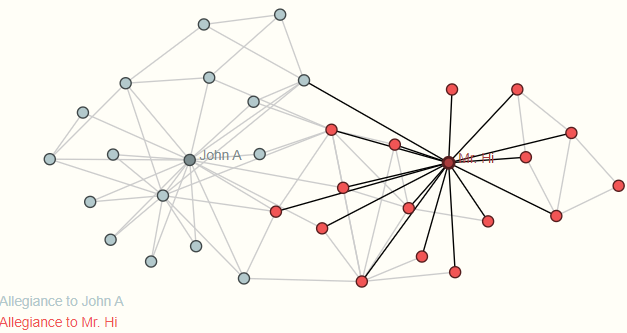
  • 对顶点判断：社交网络有两个老师分开了，学生跟随谁
image-20230525100534543
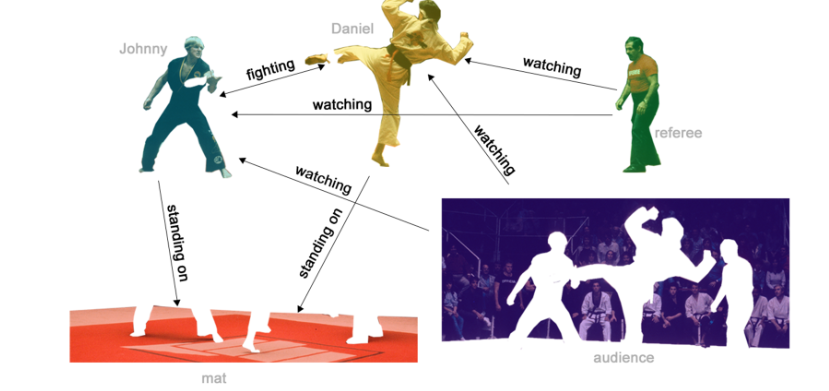
  • 对边判断：顶点是图中的物体，判断物体和物体间关系
image-20230525100522460

represent graphs

  • 顶点 边 全局信息：直接用向量，比较简单
  • 连接信息：邻接矩阵，比较大浪费空间、同一图交换两行会影响矩阵形状；邻接表
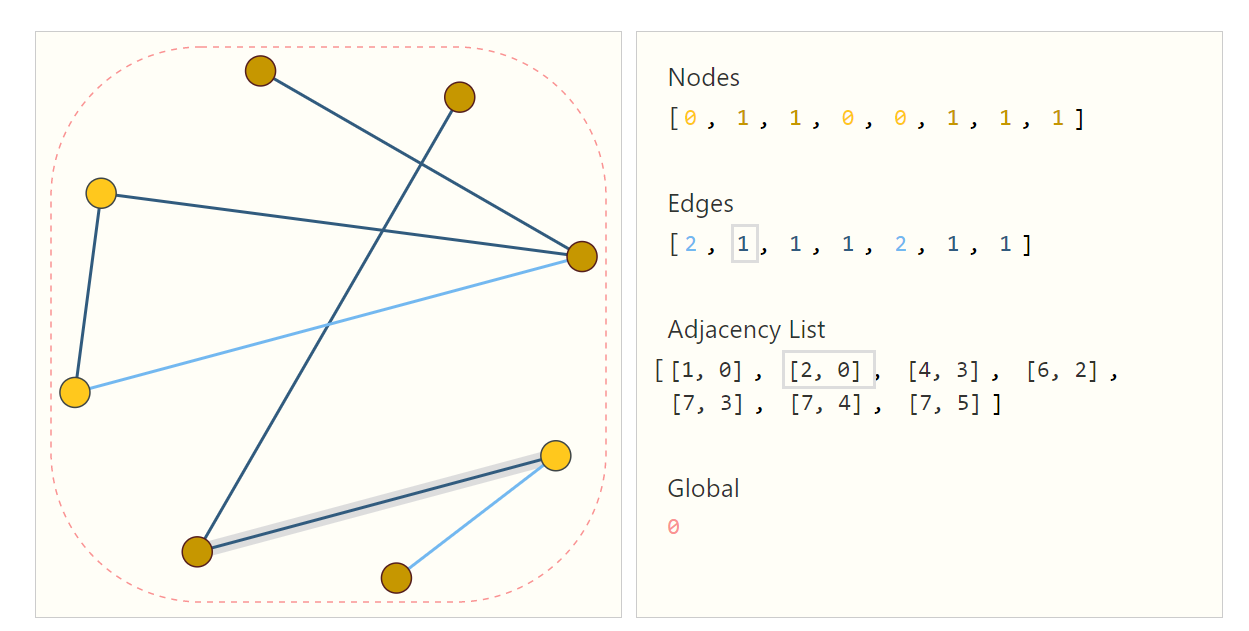
image-20230524220829767

这里用标量表示的，可替换向量

GNN：

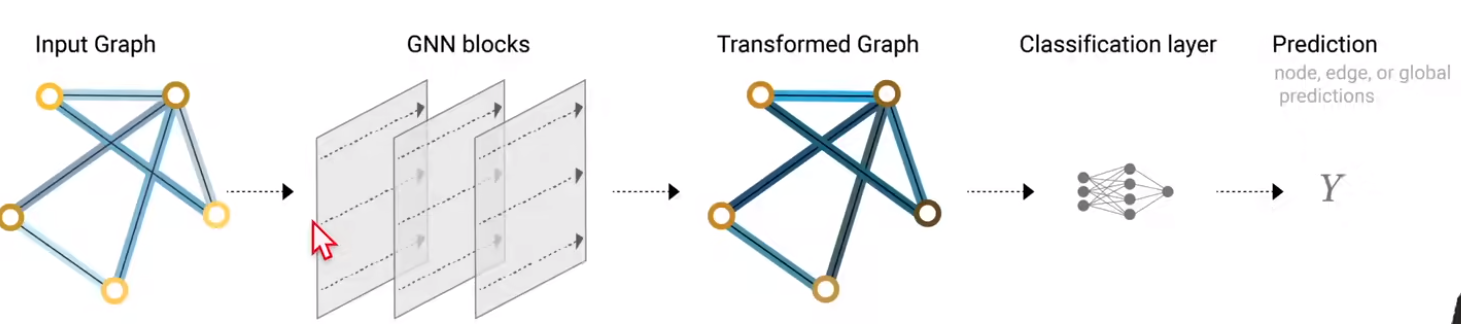
Define：对顶点、边、全局进行变换，变换满足置换不变性。输入输出都是图，对顶点、边进行变化但不改变连接性

message passing neural network

通过MLP更新顶点向量，最后对单个顶点的向量就可以通过softmax分类

image-20230524221712195

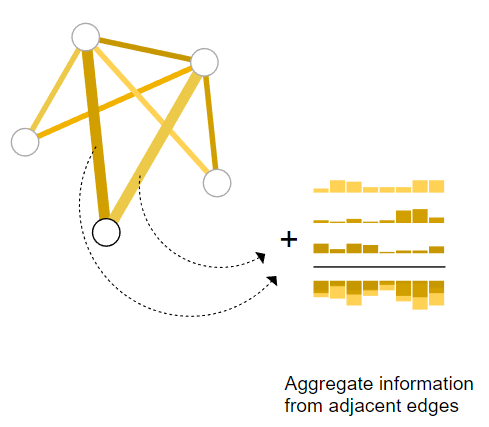
pool

可能点没有信息，但边有，在最后一层pool。pool: 边->点 。同理可以点到边

Passing messages

问题：我们没有使用图的信息(除了最后一次)，顶点和哪些边相连的。我想在GNN层中使用池化来做出更复杂的预测

点-点 或 边-边

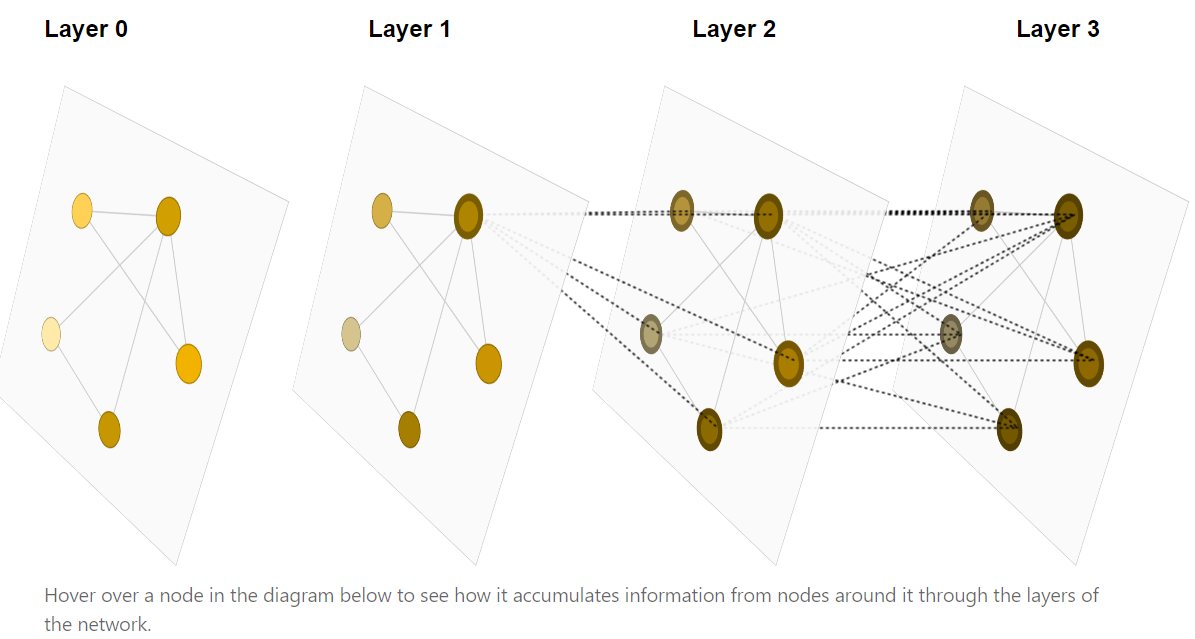
消息传递：进入mlp前，当前顶点会加上所有相邻的点，如果很多层就可以看到全局的点，如第一张图所示（像感受野）

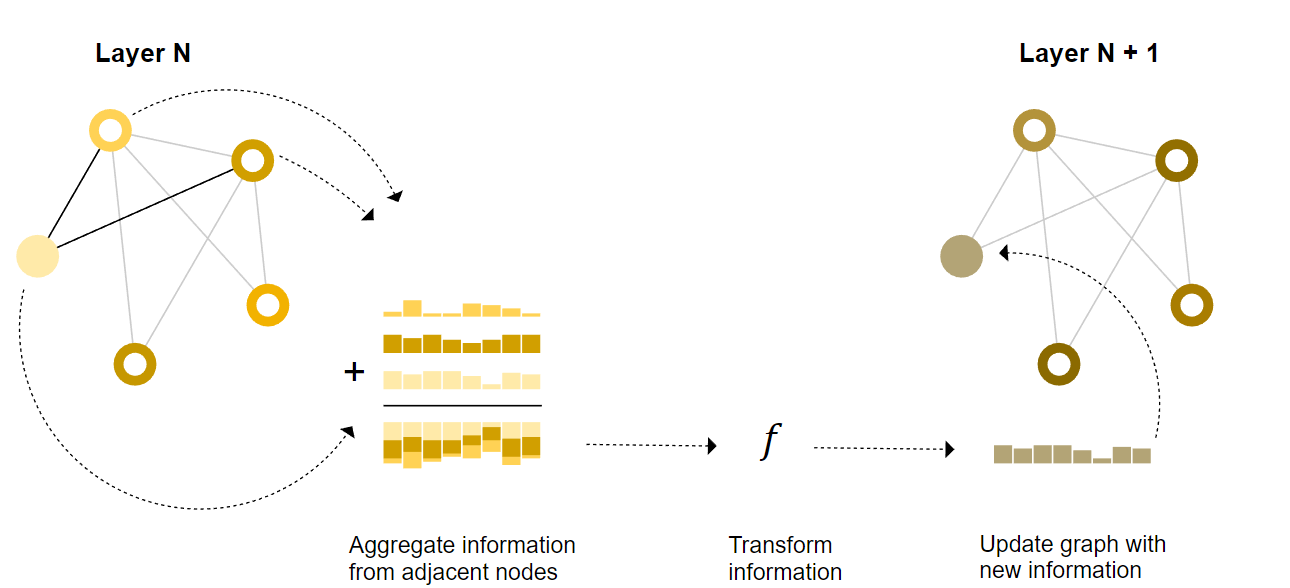
image-20230524222021997

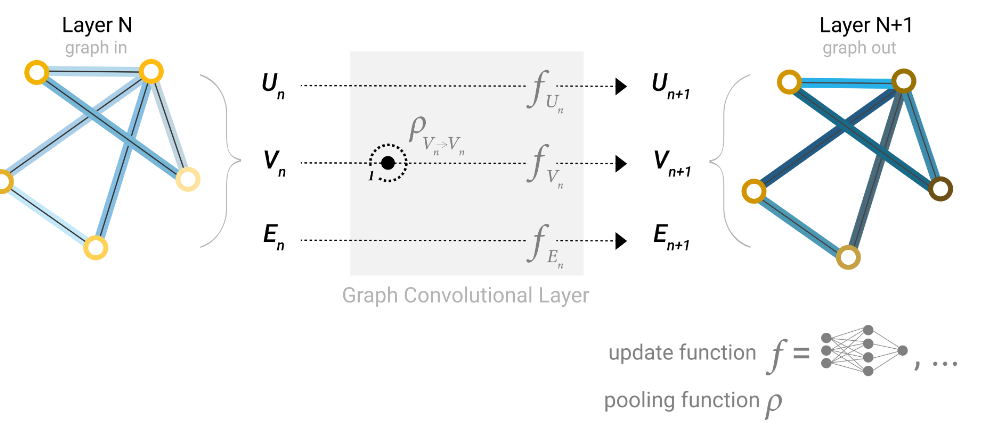
image-20230525094552106

点-边

顶点信息给边，再给边信息给点（相加、concat）

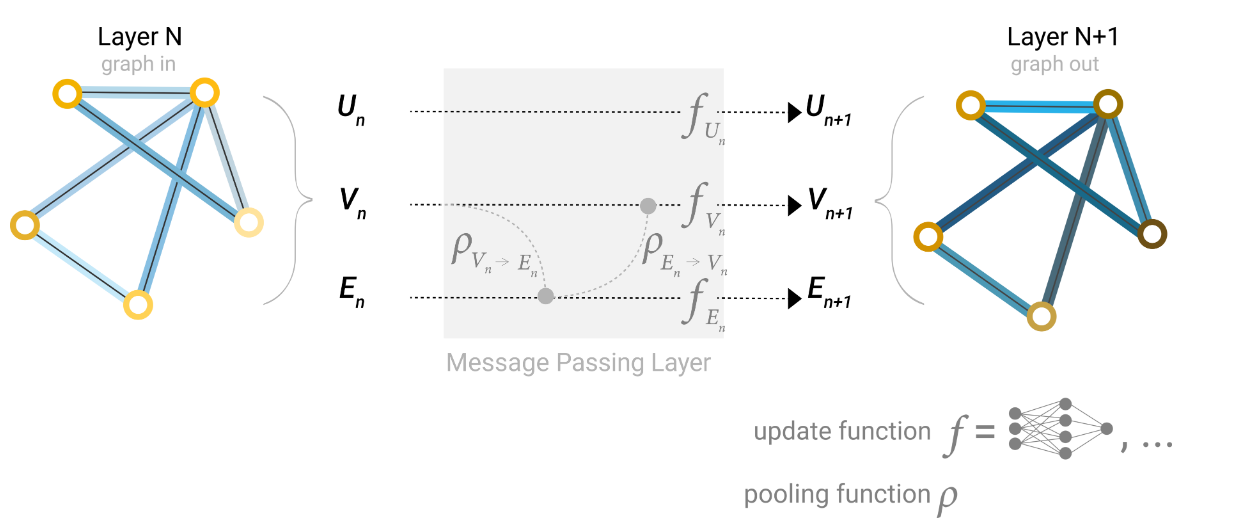
image-20230524222504445

全局信息

解决很远的节点间的消息传递问题

master node：和所有点和边相连 包含全局信息，更新时需要点边信息，点边更新时会额外加入全局

先更E(包含V，U)，再更新点（包含E，U），最后更新U（包含V，E）

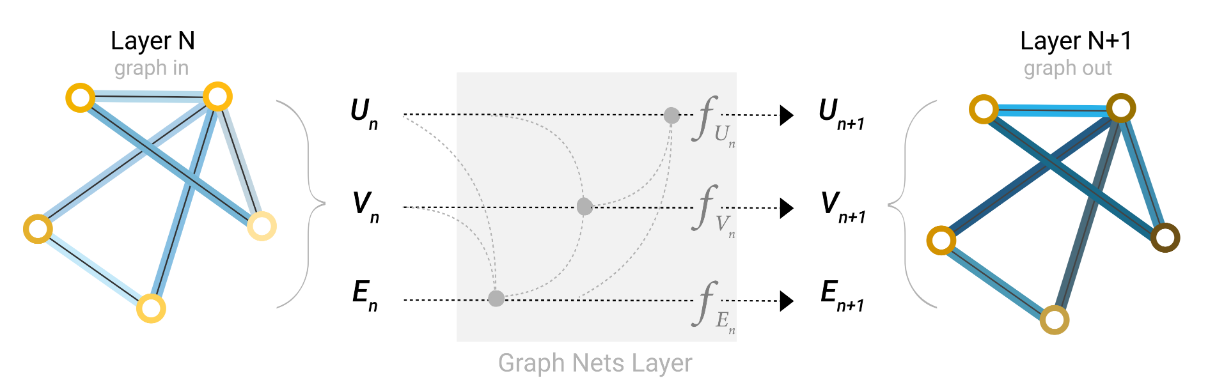
image-20230524224543319

PlayGround

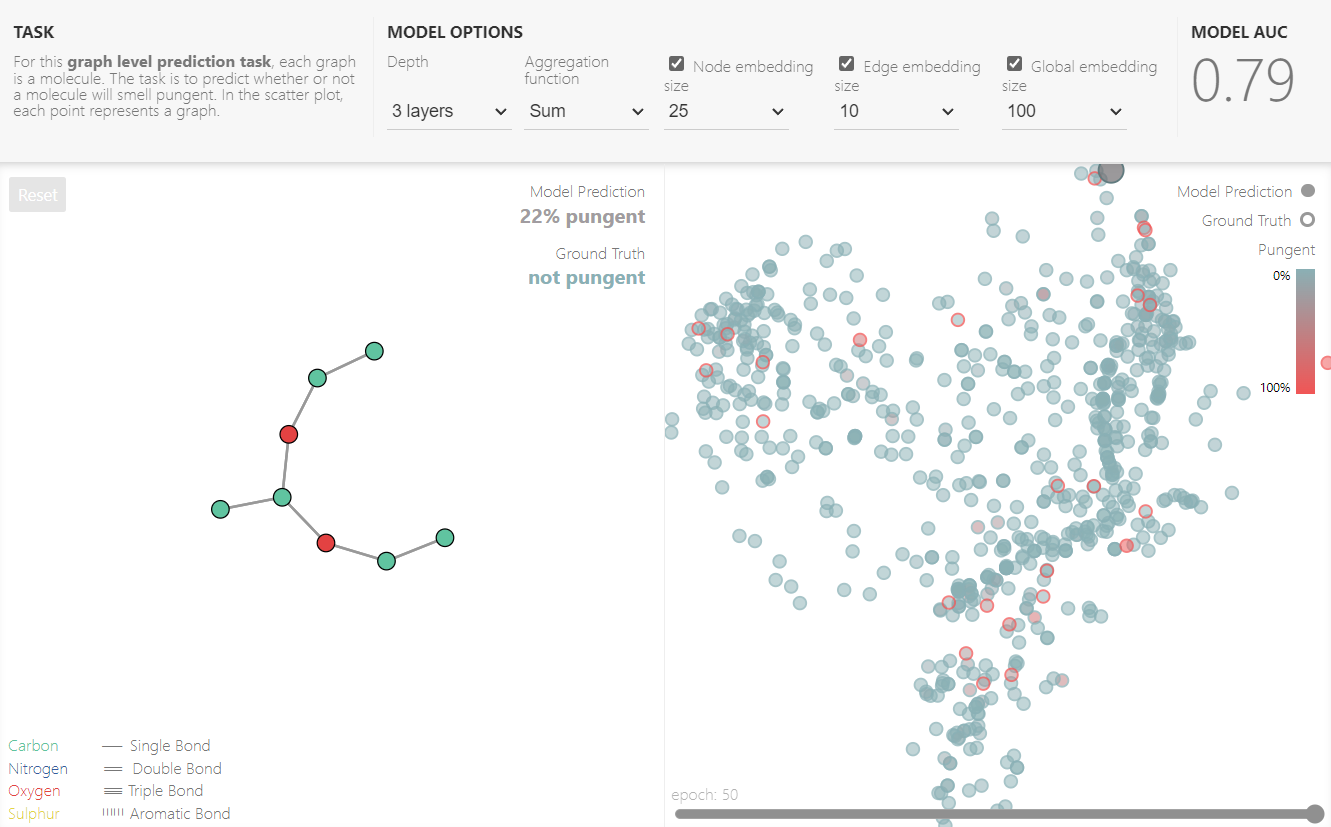
image-20230525104435625

hyperparameters：

  • Style of message passing 明显全部消息传递效果最优

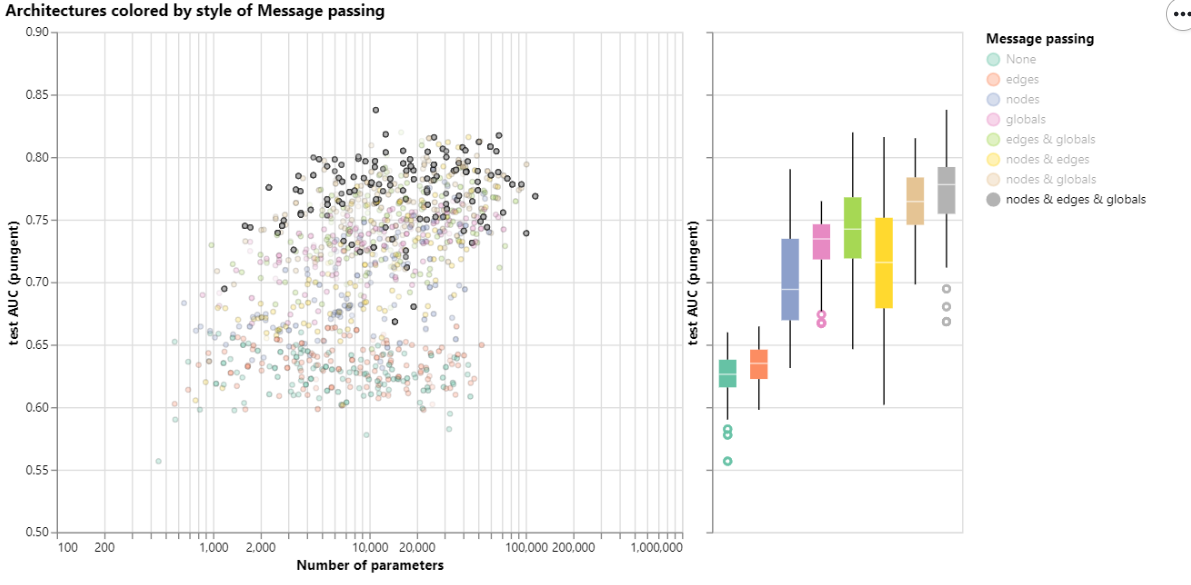
    image-20230525104737176

  • the dimensionality of embeddings

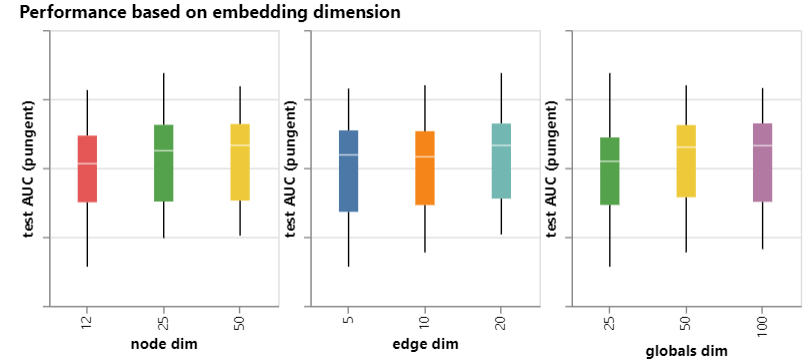
    image-20230525104343737

  • number of layers

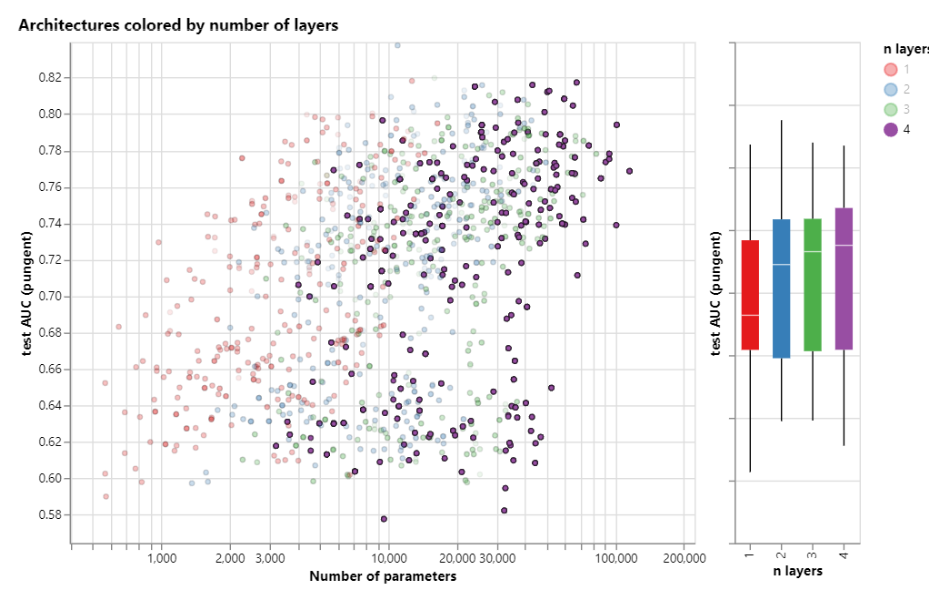
    image-20230525104804863

  • aggregation operation type

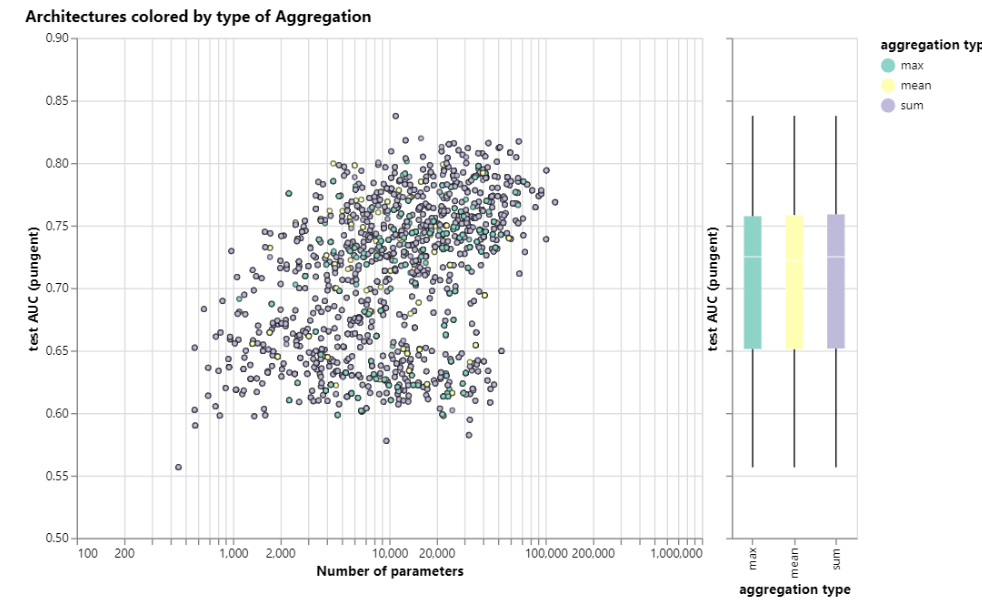
    image-20230525104615998

Into the Weeds

**Other types of graphs **

(multigraphs, hypergraphs, hypernodes, hierarchical graphs)

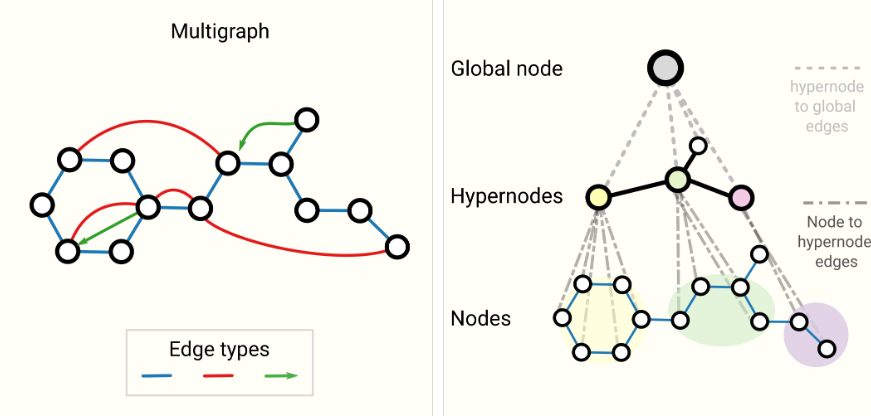
image-20230525110752250

Sampling Graphs and Batching

随机子图，随机游走多少步，随机游走再加邻居，单点BFS多少步

GCN

GCNConv 是 PyTorch Geometric 中实现 GCN 的模块，它的内部实现如下：GCNConv(x, edge_index)

image-20230525213032091

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import torch
import torch.nn as nn

class GCN(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(GCN, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, output_dim)

    def forward(self, x, adj):
        # 计算规范化的邻接矩阵
        adj = adj + torch.eye(adj.size(0))  # 加上自环
        degree = torch.sum(adj, dim=1)
        degree_sqrt = torch.sqrt(degree)
        adj_normalized = adj / degree_sqrt.unsqueeze(1) / degree_sqrt.unsqueeze(0)

        # 计算GCN层的输出
        x = self.fc1(adj_normalized @ x)
        x = torch.relu(x)
        x = self.fc2(adj_normalized @ x)

        return x

# 定义输入数据和邻接矩阵
x = torch.randn(10, 5)  # 10个节点，每个节点5维特征
adj = torch.randn(10, 10)  # 10个节点的邻接矩阵

# 创建GCN网络实例
gcn = GCN(5, 10, 2)  # 输入特征维度为5，隐藏层维度为10，输出维度为2

# 计算GCN的输出
output = gcn(x, adj)

# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(gcn.parameters(), lr=0.01)

# 训练GCN网络
for epoch in range(100):
    optimizer.zero_grad()
    output = gcn(x, adj)
    loss = criterion(output, torch.tensor([0, 1, 0, 1, 0, 1, 0, 1, 0, 1]))  # 10个节点分为两类
    loss.backward()
    optimizer.step()

Graph Attention Networks

当我们考虑一个节点及其1度相邻节点的和聚合时，我们也可以考虑使用加权和

常用的评分函数是内积，评分前常通过线性映射将节点转换为查询和关键向量，以提高评分机制的表现力。

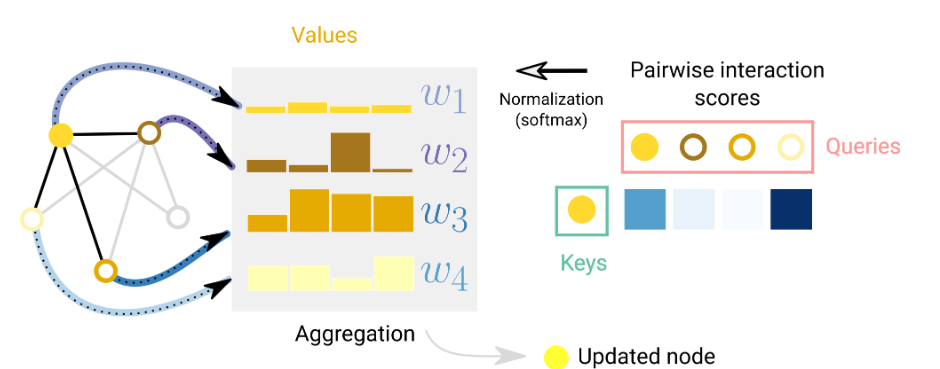
image-20230525111909292

a(l)代表着注意力分数向量；W(l)是对当前层特征做一个映射，相当于一个MLP

image-20230525122735492